Uji regresi berganda banyak sekali dipakai dalam penelitian. Pemakaian baik untuk keperluan skripsi ataupun penelitian sehari-hari. Kelebihan uji regresi adalah kemampuannya melakukan prediksi. Bagi kalangan guru sekolah atau dosen, uji regresi bisa dipakai untuk memprediksi perilaku siswa, baik dalam hal nilai atau perilaku-perilaku lainnya.
Regresi Berganda Simultan atau Standar adalah kembangan lebih lanjut dari Penelitian Korelasional. Lewat Uji Regresi hendak dilihat bagaimana suatu variabel mempengaruhi variabel lain. Regresi Berganda Simultan atau Standar juga kerap disebut Standard Multiple Regression atau Simultaneous Multiple Regression).
Dalam uji regresi berganda simultan, seluruh variabel prediktor (bebas) dimasukkan ke dalam perhitungan regresi secara serentak. Jadi, peneliti bisa menciptakan persamaan regresi guna memprediksi variabel terikat dengan memasukkan, secara serentak, serangkaian variabel bebas. Persamaan regresi kemudian menghasilkan konstanta dan koefisien regresi bagi masing-masing variabel bebas.
Selain Regresi Berganda Simultan atau Standar, ada pula Regresi Berganda Stepwise dan Regresi Berganda Hirarki. Tulisan ini hanya hendak mendalami Regresi Berganda Simultan atau Standar saja.
Regresi Berganda dengan SPSS
Regresi Berganda sangat mudah dilakukan dengan SPSS. Julie Pallant menginstruksikan dilakukannya langkah-langkah berikut ini :
- Klik Analyze --> Regression --> Linear.
- Klik variabel terikat --> Pindahkan ke kotak Dependent.
- Klik variabel bebas --> Pindahkan ke kotak Independent(s).
- Pada Method, pastikan dipilih Enter (untuk Regresi Berganda Standar).
- Klik tombol Statistics, lalu lakukan :
- Ceklis Estimates, Model fit, Descriptives, dan Collinearity diagnostics.
- Pada bagian Residual, ceklis Casewise diagnostics dan Outliers outside 3 standard deviations.
- Klik Continue.
- Klik tombol Options. Pada bagian Missing Values ceklis Exclude cases pairwise.
- Klik tombol Plots, lakukan :
- Klik *ZRESID dan tombol panah untuk memindahkannya ke kotak y-axis.
- Klik *ZPRED dan tombol panah untuk memindahkannya ke kotak x-axis.
- Klik Next
- Klik *SRESID dan tombol panah untuk memindahkannya ke kotak y-axis (untuk melihat homoskedastisitas)
- Klik *ZPRED dan tombol panah untuk memindahkannya ke kotak x-axis (untuk melihat homoskedastisitas)
- Pada bagian Standardized Residual Plots, ceklis pilihan Normal probability plot.
- Klik Continue.
- Klik tombol Save.
- Pada bagian Predicted Values, ceklis Unstandardized, Standardized, Adjusted
- Pada bagian Residuals, ceklis Standardized, Deleted, dan Studentized deleted.
- Pada bagian Distances, ceklis Mahalanobis, Cook’s, dan Leverage values.
- Pada bagian Influence Statistics, ceklis Standardized dfBeta(s) dan Standardized DiFit
- Klik Continue.
- Klik OK.
Asumsi Uji Regresi Berganda (Multiple Regression)
Menurut Julie Pallant dan Andy Field, Uji Regresi Berganda punya sejumlah asumsi yang tidak boleh dilanggar. Asumsi-asumsi Uji Regresi Berganda adalah:
1. Ukuran Sampel
Masalah berkenaan ukuran sampel di sini adalah generabilitas. Dengan sampel kecil anda tidak bisa melakukan generalisasi (tidak bisa diulang) dengan sampel lainnya. Berbeda penulis berbeda berapa sampel yang seharusnya dalam uji Regresi Berganda. Stevens (1996, p.72) merekomendasikan bahwa “untuk penelitian ilmu sosial, sekitar 15 sampel per prediktor (variabel bebas) dibutuhkan untuk mengisi persamaan uji regresi.” Tabachnick and Fidell (1996, p.132) memberi rumus guna menghitung sampel yang dibutuhkan uji Regresi, berkaitan dengan jumlah variabel bebas yang digunakan:
n > 50 + 8m
Dimana :
n = Jumlah Sampel
m = Jumlah Variabel Bebas
Jika peneliti menggunakan 5 variabel bebas, maka jumlah sampel yang dibutuhkan adalah 90 orang, dalam mana 50 ditambah ( 5 x 8) = 50 + 40 = 90.
2. Outlier
Regresi Berganda sangat sensitif terhadap Outlier (skor terlalu tinggi atau terlalu rendah). Pengecekan terhadap skor-skor ekstrim seharusnya dilakukan sebelum melakukan Regresi Berganda. Pengecekan ini dilakukan baik terhadap variabel bebas maupun terikat. Outlier bisa dihapus dari data atau diberikan skor untuk variabel tersebut yang tinggi, tetapi tidak terlampau beda dengan kelompok skor lainnya. Prosedur tambahan guna mendeteksi outlier juga terdapat pada program SPSS file mah_1. Outlier pada variabel terikat dapat diidentifikasi dari Standardised Residual plot yang dapat disetting. Tabachnick and Fidell (1996, p. 139) menentukan outlier adalah nilai-nilai Standardised Residual di atas 3,3 (atau < - 3,3).
Outlier juga bisa dicek menggunakan jarak Mahalanobis yang tidak diproduksi oleh program Regresi Berganda SPSS ini. Ia tidak terdapat dalam output SPSS. Untuk mengidentifikasi sampel mana yang merupakan Outlier, anda perlu menentukan nilai kritis Chi Square, dengan menggunakan jumlah variabel bebas yang digunakan dalam penelitian sebagai “degree of freedom-nya” atau derajat kebebasan. Pallant menggunakan Alpha 0,001 agar lebih meyakinkan, yang rinciannya sebagai berikut:
Untuk menggunakan tabel kritis Chi Square, lakukan langkah berikut:
- Tentukan variabel bebas yang digunakan dalam analisis;
- Temukan nilai di atas pada salah satu kolom berbayang; dan
- Baca melintasi kolom untuk menemukan nilai kritis yang dikehendaki.
3. Normalitas Residu
Normalitas adalah residu yang seharusnya terdistribusi normal seputar skor-skor variabel terikat. Residu adalah sisa atau perbedaan hasil antara nilai data pengamatan variabel terikat terhadap nilai variabel terikat hasil prediksi. Untuk melihat apakah residu normal atau tidak, dapat dilakukan dengan cara berikut:
- Melihat grafik Normal P-P Plot, dan
- Uji Kolmogorov-Smirnov
Pada grafik Normal P-P Plot, residu yang normal adalah data memencar mengikuti fungsi distribusi normal yaitu menyebar seiring garis z diagonal. Residu normal dari uji Kolmogorov-Smirnov adalah diperolehnya nilai p > 0,05.
Linieritas adalah residual yang seharusnya punya hubungan dalam bentuk “straight-line” dengan skor variabel terikat yang diprediksi. Homoskedastisitas adalah varians residual seputar skor-skor variabel terikat yang diprediksi seharusnya sama bagi skor-skor yang diprediksi secara keseluruhan.
4. Multikolinieritas
Uji Regresi mengasumsikan variabel-variabel bebas tidak memiliki hubungan linier satu sama lain. Sebab, jika terjadi hubungan linier antarvariabel bebas akan membuat prediksi atas variabel terikat menjadi bias karena terjadi masalah hubungan di antara para variabel bebasnya.
Dalam Regresi Berganda dengan SPSS, masalah Multikolinieritas ini ditunjukkan lewat tabel Coefficient, yaitu pada kolom Tolerance dan kolom VIF (Variance Inflated Factors). Tolerance adalah indikator seberapa banyak variabilitas sebuah variabel bebas tidak bisa dijelaskan oleh variabel bebas lainnya. Tolerance dihitung dengan rumus 1 – R2 untuk setiap variabel bebas. Jika nilai Tolerance sangat kecil (< 0,10), maka itu menandakan korelasi berganda satu variabel bebas sangat tinggi dengan variabel bebas lainnya dan mengindikasikan Multikolinieritas. Nilai VIF merupakan invers dari nilai Tolerance (1 dibagi Tolerance). Jika nilai VIF > 10, maka itu mengindikasikan terjadinya Multikolinieritas.
Hipotesis untuk Multikolinieritas ini adalah:

5. Autokorelasi
Autokorelasi juga disebut Independent Errors. Regresi Berganda mengasumsikan residu observasi seharusnya tidak berkorelasi (atau bebas). Asumsi ini bisa diuji dengan teknik statistik Durbin-Watson, yang menyelidiki korelasi berlanjut antar error (kesalahan). Durbin-Watson menguji apakah residual yang berdekatan saling berkorelasi. Statistik pengujian bervariasi antara 0 hingga 4 dengan nilai 2 mengindikasikan residu tidak berkorelasi. Nilai > 2 mengindikasikan korelasi negatif antar residu, di mana nilai < 2 mengindikasikan korelasi positif. >
Cara melakukan uji Durbin-Watson adalah, nilai Durbin-Watson hitung harus lebih besar dari batas atas Durbin-Watson tabel. Syarat untuk mencari Durbin-Watson tabel adalah Tabel Durbin-Watson. Untuk mencari nilai Durbin-Watson tabel:
- tentukan besar n (sampel) dan k (banyaknya variabel bebas).
- Tentukan taraf signifikansi penelitian yaitu 0,05.
Durbin-Watson hitung dapat dicari dengan SPSS. Nilai Durbin-Watson hitung terdapat dalam output SPSS, khususnya pada tabel Model Summary. Hipotesis untuk Autokorelasi ini adalah:
Pengambilan keputusannya adalah:
Dengan kurva normal pengambilan Durbin-Watson:
- Terima H0 jika Durbin-Watson hitung lebih besar dari ..... dan Durbin-Watson hitung lebih kecil dari 4 - .....; Artinya tidak ada Autokorelasi.
- Tolak H0 jika Durbin-Watson hitung lebih kecil dari ..... atau 4 - ..... lebih kecil dari .....; Artinya ada Autokorelasi.
6. Homoskedastisitas
Uji Regresi bisa dilakukan jika data bersifat Homoskedastisitas bukan Heteroskedastisitas. Homoskedastisitas adalah kondisi dalam mana varians dari data adalah sama pada seluruh pengamatan. Terdapat sejumlah uji guna mendeteksi gejala heteroskedastisitas misalnya uji Goldfeld-Quandt dan Park. Namun, Wang and Jain beranggapan bahwa Uji Park dapat lebih teliti dalam memantau gejala heteroskedastisitas ini. Dengan demikian, penelitian ini akan menggunakan Uji Park guna menentukan gejala heteroskedastisitas variabel-variabelnya.
Uji Park dilakukan dengan meregresikan nilai residual (Lne2) dengan masing-masing variabel independent. “The Park test suggests that if heteroscedasticity is present, the heteroscedastic varianc eσ_i^2 may be systematically related to one or more of the explanatory variables.” Rumus uji Park sebagai berikut:
Cara melakukan Uji Park adalah sebagai berikut:
- Dengan SPSS klik Analyze -->Regression --> Linear --> Masukkan variabel y ke Dependent --> Masukkan variabel x1, x2, x3, x4 ke Independent(s) --> Klik Save --> Pada Residual klik Unstandardized --> Continue --> OK
- Pada SPSS klik Data View --> Cek bahwa ada satu variabel baru bernama res_1. Ini merupakan nilai ε_i^ . Nilai ini harus dikuadratkan dengan cara (pada SPSS) klik Transform --> Compute --> Isi Target Variable dengan ε_i^2 --> Pada operasi hitung kalikan nilai ε_i^ dengan ε_i^ . Pada Variable View SPSS muncul variabel baru bernama ε_i^2.
- Dengan SPSS, tepatnya menu Transform --> Compute lakukan perubahan nilai ε_i^2, X1, X2, X3, X4 ke dalam bentuk logaritma natural (Ln) [caranya dengan Klik Ln lalu pindahkan variabel] Ln(ε_i^2 ) yaitu regresi unstandardized residual pada Target Variable dinamai Lnei2; X1 yaitu variabel x1 pada Target Variable dinamai Lnx1; X2 yaitu variabel x2 pada Target Variable dinamai Lnx2; x3 yaitu variabel x3 pada Target Variable dinamai Lnx3; x4 yaitu variabel x4 pada Target Variable dinamai Lnx4.
- Setelah diperoleh nilai variabel-variabel baru Lnei2, LnX1, LnX2, LnX3, dan LnX4.
- Lakukan uji regresi kembali secara satu per satu.
- Pertama, klik Analyze --> Regression>Linear --> Masukkan variabel Lnei2 ke kotak Dependent --> Masukkan variabel LnX1 ke Independent(s) --> OK. Sementara hasil belum dihiraukan.
- Kedua, klik Analyze --> Regression --> Linear --> Variabel Lnei2 masih ada di Dependent, biarkan > Keluarkan LnX1 dan masukkan LnX2 ke Independent(s) > OK. Sementara hasil belum dihiraukan.
- Ketiga, klik Analyze --> Regression --> Linear --> Variabel Lnei2 masih ada di Dependent, biarkan > Keluarkan LnX2 dan masukkan LnX3 ke Independent(s) > OK. Sementara hasil belum dihiraukan.
- Keempat, klik Analyze --> Regression --> Linear --> Variabel Lnei2 masih ada di Dependent, biarkan > Keluarkan LnX3 dan masukkan LnX4 ke Independent(s) > OK. Sementara hasil belum dihiraukan.
- Perhatikan Output SPSS. Pada output, terdapat hasil perhitungan Park bagi variabel x1, x2, x3 dan x4, tepatnya adalah hasil uji Lnei2 dengan LnX1, dan uji Lnei2 dengan LnX2, uji Lnei2 dengan LnX3, dan uji Lnei2 dengan LnX4.
- Peneliti akan memperbandingkan apa yang tertera di tabel Coefficients, yaitu nilai t.
- Guna memastikan apakah ada gejala heteroskedastisitas, peneliti akan memperbandingkan nilai thitung dengan ttabel. Nilai ttabel dapat dicari pada Tabel t, yaitu dengan menentukan df = n - 4 . n adalah jumlah sampel dan 4 karena jumlah variabel independen penelitian adalah 4. Sehingga nilai df = 48 – 4 = 44. Dalam taraf 0,05 uji yang dilakukan adalah 2 sisi sehingga singnifikansi pada tabel adalah 0,025.
Dengan mempertemukan nilai 46 dan 0,025 dan uji 2 sisi pada taraf 95% (0,025) pada Tabel t diperoleh nilai t tabel penelitian sebesar ......
Hipotesis yang diajukan mengenai masalah homoskedastisitas ini sebagai berikut:
Alternatif Uji Homoskedastisitas Jika Uji Park dianggap Terlampau Rumit
Jika uji Park dianggap terlampau rumit, maka pengujian alternatif dapat ditempuh guna melihat apakah terjadi Homoskedastisitas atau Heteroskedastisitas.
Caranya dengan melihat grafik persilangan SRESID dengan ZPRED pada output hasil SPSS. Caranya sebagai berikut:
- Klik Analyze --> Regression --> Linear
- Klik Plot.
- Isikan SRESID pada y-axis dan ZPRED pada x-axis.
- Klik Continue. Perhatikan grafik scatterplot. Ingat, Homoskedastisitas terjadi jika varians dari residual satu pengamatan ke pengamatan lain tetap atau sama. Heteroskedastisitas terjadi jika varians dari residual satu pengamatan ke pengamatan lain tidak sama atau tidak tetap.
Homoskedastisitas terjadi jika tidak terdapat pola tertentu yang jelas, serta titik-titik menyebar di atas dan di bawah angka 0 pada sumbu Y. Heteroskedastisitas terjadi jika terdapat titik-titik memili pola tertentu yang teratur seperti bergelombang, melebar kemudian menyempit.
Interpretasi Hasil Uji Regresi Berganda
Setelah uji Regresi Berganda selesai dilakukan, peneliti harus melakukan interpretasi. Rumus Regresi Berganda (standar) adalah sebagai berikut:
Setelah pengujian Regresi Berganda dengan SPSS selesai, hal-hal penting untuk interpretasi adalah apa yang tercantum pada tabel-tabel pada output SPSS.
Tabel Descriptives
Pada tabel Descriptive dapat dilihat nilai Standar Deviasi. Nilai ini terdapat pada kolom Std. Deviation. Nilai ini nanti akan diperbandingkan dengan nilai Std. Error of the Estimate.
Tabel Model Summary
Tabel ini memberi informasi seberapa baik model analisis kita secara keseluruhan, yaitu bagaimana 4 variabel bebas mampu memprediksikan 1 variabel terikat, dengan rincian sebagai berikut ini:
Kolom Model. Menunjukkan berapa buah model analisis yang kita bentuk.
Kolom R. Menunjukkan seberapa baik variabel-variabel bebas memprediksikan hasil (multiple correlation coefficient). Kisaran nilai R adalah 0 hingga 1. Semakin nilai R mendekati angka 1, maka semakin kuat variabel-variabel bebas memprediksikan variabel terikat. Namun, ketepatan nilai R ini lebih disempurnakan oleh kolom Adjusted R Square yang merupakan koreksi atas nilai R.
Kolom Adjusted R Square. Fungsinya menjelaskan apakah sampel penelitian mampu mencari jawaban yang dibutuhkan dari populasinya. Kisaran nilai Adjusted R Square adalah 0 hingga 1. Pedoman interpretasi atas nilai Adjusted R Square adalah sebagai berikut:

Kalikan Adjusted R2 dengan 100% maka akan diperoleh berapa % varians tiap sampel pada variabel terikat bisa diprediksi oleh variabel-variabel bebas secara bersama-sama (simultan).
Std. Error of the Estimate. Kolom ini menjelaskan seberapa kuat variabel-variabel bebas bisa memprediksi variabel terikat. Nilai Std. Error of the Estimate diperbandingkan dengan nilai Std. Deviation (bisa dilihat pada tabel Descriptives). Jika Std. Error of the Estimate < Std. Deviation, maka Std. Error of the Estimate baik untuk dijadikan prediktor dalam menentukan variabel terikat. Jika Std. Error of the Estimate > Std. Deviation, maka Std. Error of the Estimate tidak baik untuk dijadikan prediktor dalam mementukan variabel terikat.
Durbin-Watson. Kolom ini digunakan untuk mengecek uji asumsi Autokorelasi. Bagaimana variabel bebas yang satu berkorelasi dengan variabel bebas lainnya. Durbin-Watson ini digunakan dalam uji asumsi Regresi sebelumnya.
Tabel Coefficients
Pada tabel Coefficient, mohon perhatikan lalu jelaskan nilai-nilai yang tertera pada kolom-kolom berikut ini:
Model. Kolom ini menjelaskan berapa banyak model analisis yang dibuat peneliti. Pada kolom ini juga terdapat nama-nama variabel bebas yang digunakan dalam penelitian. Variabel-variabel tersebut diberi label “Constant” yaitu nilai konstanta yang digunakan dalam persamaan uji Regresi Berganda (a).
Unstandardized Coefficient. Kolom ini terdiri atas b dan Std. Error. Kolom b menunjukkan Koefisien b, yaitu nilai yang menjelaskan bahwa Y (variabel terikat) akan berubah jika X (variabel bebas) diubah 1 unit.
Standardized Coefficients. Pada kolom ini terdapat Beta. Penjelasan sebelumnya mengenai nilai b punya masalah karena variabel-variabel kerap diukur menggunakan skala-skala pengukuran yang berbeda. Akibatnya, kita tidak bisa menggunakan nilai b guna melihat variabel-variabel bebas mana yang punya pengaruh lebih kuat atas variabel terikat. Misalnya, jika variabel yang diteliti adalah jenis kelamin yang punya skala minimal 1 dan maksimal 2 dan pengaruhnya terhadap sikap yang skalanya minimal 1 dan maksimal 6, nilai b diragukan efektivitas prediksinya. Ini akibat nilai yang diperolehnya rendah atas pengaruh perbedaan skala pengukuran. Untuk memastikan pengaruh inilah maka nilai Beta dijadikan patokan. Nilai Beta punya kisaran 0 hingga 1, di mana semakin mendekati 1 maka semakin berdampak besar signifikansinya.
Sig. Kolom ini menjelaskan tentang signifikansi hubungan antar variabel bebas dengan variabel terikat. Nilai Sig. ini sebaiknya adalah di bawah 0,05 (signifikansi penelitian).
Tolerance. Kolom ini menjelaskan banyaknya varians pada suatu variabel yang tidak bisa dijelaskan oleh variabel prediktor lainnya. Kisarannya 0 hingga 1, di mana semakin mendekati 1 maka semakin mengindikasikan prediktor-prediktor lain tidak bisa menjelaskan varians di variabel termaksud. Nilai yang semakin mendekati 0 artinya hampir semua varians di dalam variabel bisa dijelaskan oleh variabel prediktor lain. Nilai Torelance sebaiknya ada di antara 0,10 hingga 1.
Tabel ANOVA
Sig. Tabel ANOVA menunjukkan besarnya angka probabilitas atau signifikansi pada perhitungan ANOVA. Nilai yang tertera digunakan untuk uji kelayanan Model Analisis [dimana sejumlah variabel x mempengaruhi variabel y] dengan ketentuan angka probabilitas yang baik untuk digunakan sebagai model regresi harus < 0,05. Nilai ini bisa dilihat pada kolom Sig. Jika Sig. < 0,05, maka Model Analisis dianggap layak. Jika Sig. > 0,05, maka Model Analisis dianggap tidak layak.
Pengambilan Keputusan dengan Tabel ANOVA
Dalam Regresi Berganda, hal utama yang hendak dilihat adalah apakah serangkaian variabel bebas secara serentak mempengaruhi variabel terikat. Dalam output SPSS ini bisa ditentukan lewat tabel ANOVA.
Pada tabel ANOVA terdapat kolom F. Nilai yang tertera pada kolom F tersebut disebut sebagai F hitung. F hitung ini diperbandingkan dengan F tabel. Peraturannya:
Persoalannya, bagaimana menentukan F tabel? F tabel dapat ditentukan dengan cara:
- Tentukan signifikansi penelitian yaitu 0,05 (uji 2 sisi jadi 0,025.
- Tentukan df1. Df1 diperoleh dari jumlah variabel bebas
- Tentukan df2. Df2 diperoleh dari n – k – 1 = 48 – 4 – 1 = 43.
- Cari angka 43 dan 4 dalam tabel F untuk signifikansi 0,025.
- Dengan Excel, ketikkan rumus =FINV(0,05;4;43)
Selain perbandingan nilai F, penerimaan atau penolakan Hipotesis juga bisa menggunakan nilai Sig. pada tabel ANOVA. Peraturannya:
Koefisien Determinasi
Dalam uji Regresi Berganda, Koefisien Determinasi digunakan untuk mengetahui persentase sumbangan pengaruh serentak variabel-variabel bebas terhadap variabel terikat. Untuk itu, digunakan angka-angka yang ada pada Tabel Model Summary.
Cara menentukan Koefisien Determinasi sangatlah mudah. Peneliti tinggal melihat nilai pada kolom R2 dikalikan 100%. Misalnya nilai R2 adalah 0,7777. Dengan demikian Koefisien Determinasinya = 0,7777 x 100% = 77,77%. Jadi, secara serentak variabel-variabel bebas mempengaruhi variabel terikat sebesar 77,77%. Sisanya, yaitu 100 – 77,77% = 22,23% ditentukan oleh variabel-variabel lain yang tidak disertakan di dalam penelitian.
Koefisien Regresi Parsial
Koefisien Regresi Parsial menunjukkan apakah variabel-variabel bebas punya pengaruh secara parsial (terpisah atau sendiri-sendiri) terhadap variabel terikat?
Pada Tabel Coefficient, pengujian Hipotesis akan dilakukan. Uji hipotesis dilakukan dengan menggunakan Uji t. Pernyataan Hipotesis yang hendak diuji sebagai berikut:
Nilai t hitung bisa dilihat pada kolom t bagi masing-masing variabel bebas.
Nilai t tabel bisa dicari dengan cara berikut ini:
- α = 0,05; untuk uji 2 sisi = 0,025
- Degree of Freedom (df) = jumlah sampel – jumlah variabel bebas – 1 (angka 1 adalah konstanta) = 48 – 4 – 1 = 43.
- Cari persilangan antara df = 43 dan 0,025.
- Pencarian nilai t tabel dengan Excel mudah sekali. Ketik rumus =tinv(0,05;43).
-----------------------------------------
Daftar Pustaka
- Andi Field, Discovering Statistics using SPSS: And Sex Drug and Alcohol, Second Edition (London: SAGE Publication, 2005)
- Daniel Muijs, Doing Quantitative Research in Education with SPSS (London: SAGE Publication Ltd., 2004)
- George C.S. Wang and Chaman L. Jain, Regression Analysis: Modelling and Forecasting (New York: Graceway Publishing Company, 2003)
- Jonathan Sarwono, Statistik Itu Mudah: Panduan Lengkap untuk Melakukan Komputasi Statistik Menggunakan SPSS 16 (Yogyakarta: Penerbit ANDI, 2009)
- Julie Pallant, SPSS Survival Manual: A Step by Step Guide to Data Analysis using SPSS for Windows, Third Edition (Berkshire: McGraw-Hill and Open University Press, 2007)
- Nancy L. Leech, Karen C. Barrett, George A. Morgan, SPSS for Intermediate Statistics: Use and Interpretation, Second Edition (New Jersey: Lewrence Erlbaum Associates, Publishers, 2005)
- Sarah Boslaugh and Paul Andrew Watter, Statistics in a Nutshell: A Desktop Quick Reference (Sebastopol: O’Reilly Media, Inc., 2008)
- Simon Washington, Matthew G. Karlaftis and Fred L. Mannering, Statistical and Econometric Methods for Transportation Data Analysis, (Boca Raton : Chapman & Hall/CRC, 2003)
- Tony Wijaya, Analisis Data Penelitian Menggunakan SPSS (Yogyakarta: Penerbit Universitas Atma Jaya Yogyakarta, 2009)
cara uji regresi berganda dengan spss menafsirkan output hasil spss arti tabel summary koefisien determinasi regresi parsial mengolah hasil spss

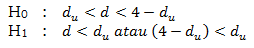







No comments:
Post a Comment